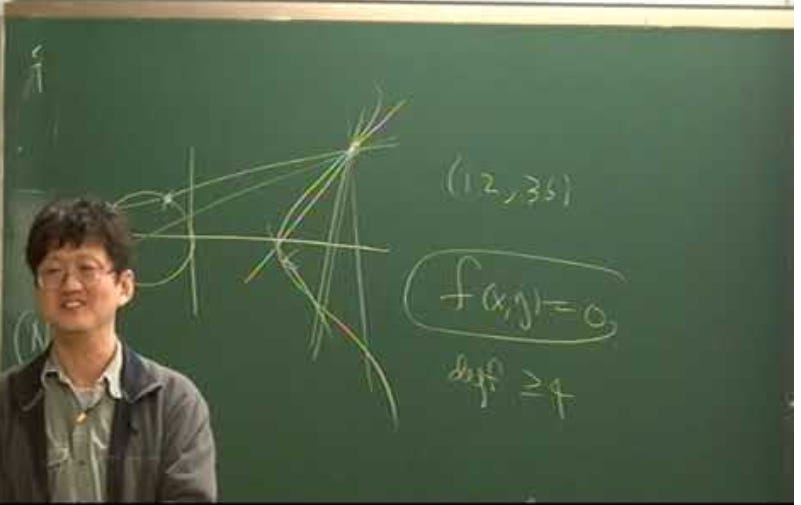I wrote this essay in 2018 and it was originally published on Gizadeathstar.com. I wanted to add material and share it with you as I am continuing my research in this area. The topic concerns some of the most profound problems in science where progress is made by the greatest thinkers. -Ed.
Mathematicians and physicists, though they use many of the same tools, exist in a kind of cultural cold war. When a mathematician writes a scientific paper, he is unable to include references to mathematical physics in his papers because “its only physics” and is not “rigorous.” At the same time, physicists hungrily borrow from the math tool set, while butchering its purity and remaining aloof to the puzzles which occupy the brightest minds in the math field.
The Science Cold War
When I was in college, there was something of an "interservice rivalry" (Army v. Navy) between the two groups. The mathematicians would point out how some physicist incorrectly applied math in some theory or other. And the physicists distrusted mathematicians' lack of concern with the applicability of their work to problems "in the real world."
But many of us, this author included, bathed in the intuition that there was some core idea that would make it clear that math and physics were, at some very great level, both part of a deeper holistic order, still invisible to the methods of today.
In general, physicists are more likely to believe that math and physics are deeply related. That said, mathematicians' aversion to physics grew out of a real concern that the messiness of theory and the imperfection of experimental method would distract them from their attentions to pure reason. To a mathematician, the real world is a sloppy mess.
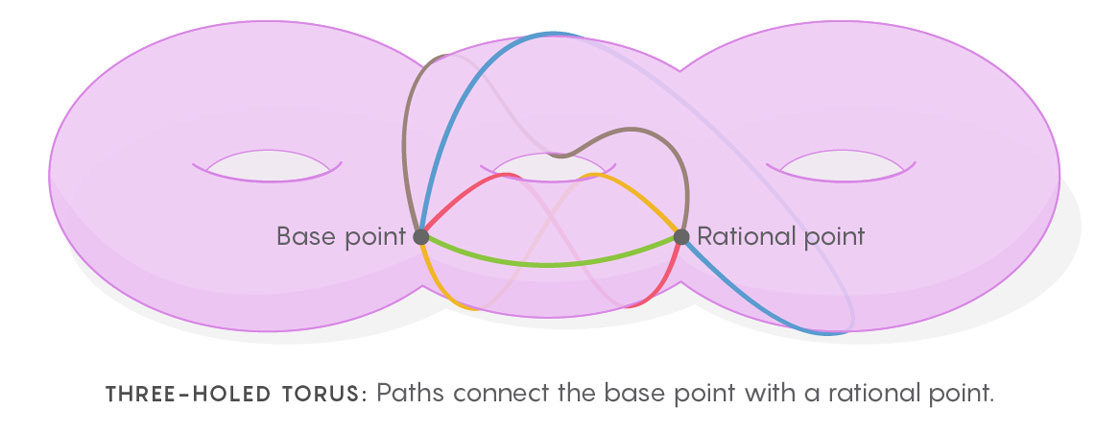
Well, in a 2017 issue of Quanta Magazine, one of the world's top number theorists, Minhyon Kim, of the University of Oxford, it has been reported that a unique and powerful theory that ties some elements in physics directly to the theory of real numbers has been revealed. This is a big deal even though it happened four years ago.
Here is the link to this rather long but very well written piece in Quanta Magazine.
Secret Link Uncovered Between Pure Math and Physics.
The author states:
"Over the past decade Kim has described a very new way of looking for patterns in the seemingly patternless world of rational numbers. He’s described this method in papers and conference talks and passed it along to students who now carry on the work themselves. Yet he has always held something back. He has a vision that animates his ideas, one based not in the pure world of numbers, but in concepts borrowed from physics. To Kim, rational solutions are somehow like the trajectory of light."
The new theory connects a type of field theory (which means objects in the presence of forces in a space), gauge theory, and the geometric representation of the real numbers. For example, if you have an equation, x squared plus y squared = 1, the solutions can be mapped as dots on a circle, but the distribution of those points on a circle will be all over the place, which means that symmetry suffers. Reduced symmetry makes comprehensive theories difficult. Can you imagine Einstein's relativity without a clear symmetry between the effects of mass and energy on space? It would not work.
In order to increase symmetry, Kim created a special "space of spaces” - gauge theory - that creates more opportunities for real number symmetry to be exposed. Interestingly, Dr. Kim describes in his work that a solution to his problem is analogous to the trajectory of light, which relies on what physicists call "the principle of least action", meaning the photon will always take the quickest path, like a commuter seeking out all the shortcuts on the way home. Dr. Kim firmly believes that an analogous principle lies at the heart of real numbers.
Squishy Foundations and The Frantic Effort
Most students would be surprised to learn that much of the math they learn is not fully understood. Rene Decartes once quipped, when he deconstructed Euclid's elements, that the ancient geek relied on a method of analysis that has since been lost. He referred to this hidden math, this magician’s sleight of hand, as a “certain, wicked, slyness.” These obscure forms of analysis are critical to getting the squishy out of the foundation.
An intense and prolonged effort has existed, hidden from view, to recover that lost analysis, covering centuries, involving the greatest minds and power centers, especially in Europe. In fact, so great was the effort that royal houses of Europe went as far as China and its analogical (pictograph characters) language for clues. Even 17th century fiction writers went on intellectual ‘voyages’ in search of characteristica universalis, the universal language of thought.1
What were they so desperate to find? And why not fully out in the open?
The Relatedness of Things
The door to the deeper picture here, as you may observe, is that Dr. Kim noticed the analogy between light and real number representations. And this suggests to me that we consider Dr. Kim's work in relation to Leibniz's Characteristica Universalis, and Kurt Goedel's incompleteness theorem.
Dr. Kim has taken us a few steps closer to comprehending a set of universal principles for holistic systems. For me, When implicate connections are revealed between two very disparate disciplines; that's a clue that we are getting closer to Gottfried Leibnitz's long ago vision. Leibniz was a 17th century attorney, natural philosopher and mathematician, who participated in the drafting of the Treaty of Westphalia, and was the inventor of the usable calculus and symbolic notation which we still use today.
Leibniz thought that if the universal principles, forms and methods of thought itself could be uncovered, a form of analysis could be generated to provide a universal analysis of situation that could be applied anywhere that thought could be applied. If it sounds a bit like artificial intelligence, that's because they are vastly different approaches to a similar problem. But Leibnitz himself was aiming for a universal language of thought, of proof; a system to know if propositions were true, and to build machines to do the calculations, in 1689! Leibniz was the first to envision automated processing, e.g. computing machines, that could help with thinking. Stop and think for a minute how powerful such a system and method would be.
It would not be until the later part of the twentieth century, when Noam Chomsky's grammar would grace us with its giant piece of the puzzle, as pointed out by Joseph P. Farrell, that a fuller measure of the process of thought was reached, but that is a subject for another time.
Dr. Kim’s theory uses the physics principle of least action and I find it interesting and coincident that it was Leibniz who tip-toed close to the “principle of least action” in his foundational works on the philosophy of space.2 Leibniz was convinced that a core principle of physics was efficient ‘action’. For that, Leibniz, who patiently struggled for a third of a century to build symbolic systems of thought using theological, philosophical, metaphysical, epistemological, logical and physical content in a consistent, holistic method and system - would be quite interested in the findings of Dr. Kim.
This author is also reminded of Dr. David Bohm’s work on hidden variables in Quantum Theory. The hidden order and tools for tackling it were advanced by Bohm and are analogous to some of what Dr. Kim, is doing. Will we discover, as logicians and mathematicians edge closer, a new wrinkle of implicate order?3
When high mathematics, topology, quantum theory and the physics of light are seen in the same framework, to me means that progress is being made. Perhaps in fifty years, or two centuries, Dr. Kim's intellectual descendants will discover that the real numbers are in fact a kind of physics, which I suspect Dr. Kim already knows and I believe.
We will at some point fully identify the method and system of pure thought and how to apply it to the universe at large? To arrive sooner, Dr. Kim’s cross-disciplinary vision should be adopted by others.
Leibniz did say that if it could be thought, if it was possible, it had achieved reality. In my view, that mathematics and physics might someday reconverge is most interesting and should be pursued aggressively. And the science that would result from its objective beauty would be astounding indeed.
Paul Cornelius, PhD, Language in 17th Century Voyages, Columbia University, 1963, published by Library Priveé, Geneva.
See Geometry and Monadology and the Philosophy of Space, Vincenzo di Risi, 2007, Birkhauser
“Implicate”, or hidden higher order.